Will Yuan's Blog

Posted on Word count in article: 285 Reading time ≈ 1 mins.

SQLite is a C library that provides a lightweight disk-based database. More information can be found here: https://www.sqlite.org/index.html.

We can use the sqlite3 library in Python. More information about this library: https://docs.python.org/3/library/sqlite3.html.

Here are some sample codes for the commonly used functions of this library:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import sqlite3

# Create a database in the current working directory
conn = sqlite3.connect('my_db.db')

# Create a database cursor
cursor = conn.cursor()

# Create a table
cursor.execute('''
CREATE TABLE IF NOT EXISTS users (
    id INTEGER PRIMARY KEY AUTOINCREMENT,
    name TEXT NOT NULL,
    age INTEGER
)
''')

# Commit changes
conn.commit()

# Insert a single record
cursor.execute("INSERT INTO users (name, age) VALUES (?, ?)", ("A", 30))

# Insert multiple records
new_users = [("B", 20), ("C", 10)]
cursor.executemany("INSERT INTO users (name, age) VALUES (?, ?)", new_users)
conn.commit()

# Query all users
cursor.execute("SELECT * FROM users")

print('All users:')
user_info_1 = cursor.fetchall()
print(user_info_1)

# Update a record
cursor.execute("UPDATE users SET age = ? WHERE name = ?", (100, "A"))
conn.commit()

print('After update:')
cursor.execute("SELECT * FROM users")
# fetchall() does not automatically refresh the data, it only reads the results of the last execute()
user_info_2 = cursor.fetchall()
print(user_info_2)

#  Delete a record
cursor.execute("DELETE FROM users WHERE name = ?", "A")
conn.commit()

print('After delete a record:')
cursor.execute("SELECT * FROM users")
user_info_3 = cursor.fetchall()
print(user_info_3)

# Delete all records
cursor.execute("DELETE FROM users")
conn.commit()

print('After delete all records:')
cursor.execute("SELECT * FROM users")
user_info_4 = cursor.fetchall()
print(user_info_4)

# Close the database connection
conn.close()

The output is as follows:

Read more »

Posted on Word count in article: 1.6k Reading time ≈ 6 mins.

The official manual gives sample code for using OR-Tools to solve problems:

https://developers.google.com/optimization/routing/vrp

The python code is as follows:

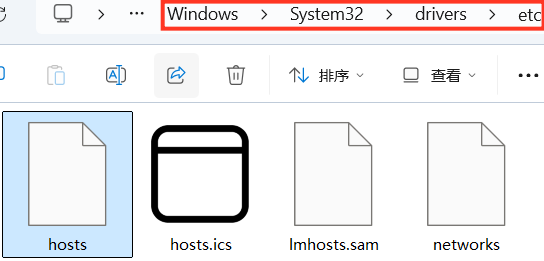
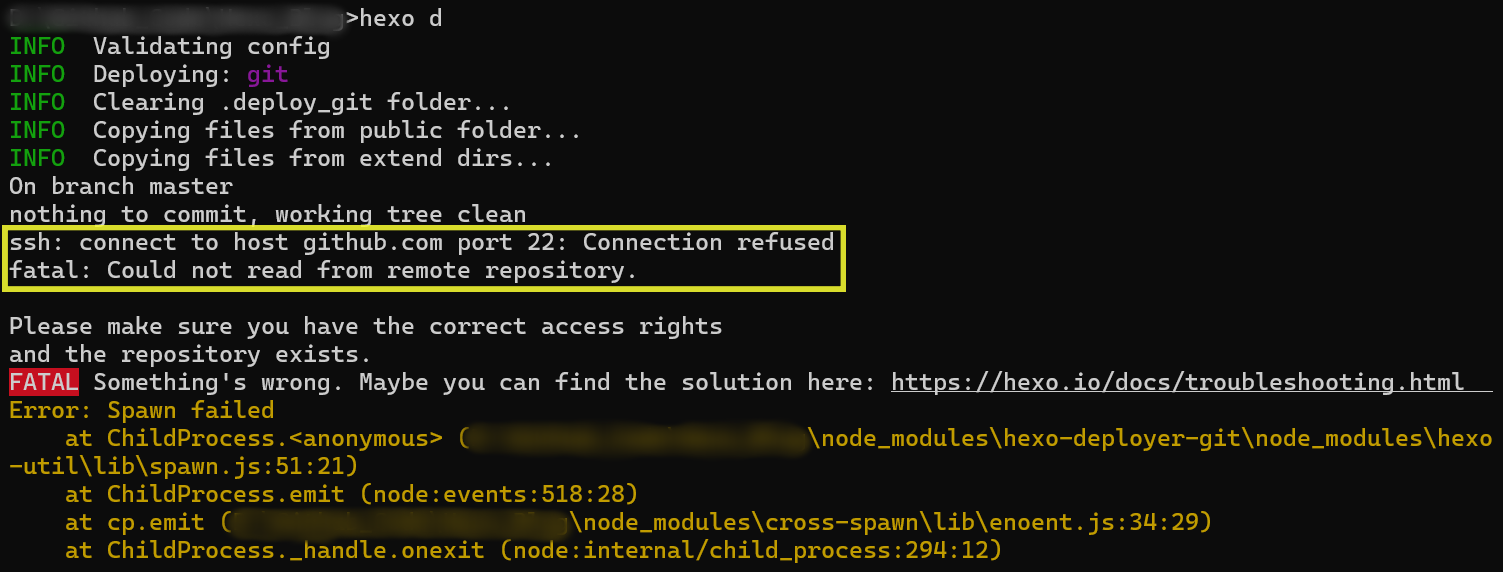
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
"""Simple Vehicles Routing Problem (VRP).

   This is a sample using the routing library python wrapper to solve a VRP
   problem.
   A description of the problem can be found here:
   http://en.wikipedia.org/wiki/Vehicle_routing_problem.

   Distances are in meters.
"""

from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp


def create_data_model():
    """Stores the data for the problem."""
    data = {}
    data["distance_matrix"] = [
        # fmt: off
        [0, 548, 776, 696, 582, 274, 502, 194, 308, 194, 536, 502, 388, 354, 468, 776, 662],
        [548, 0, 684, 308, 194, 502, 730, 354, 696, 742, 1084, 594, 480, 674, 1016, 868, 1210],
        [776, 684, 0, 992, 878, 502, 274, 810, 468, 742, 400, 1278, 1164, 1130, 788, 1552, 754],
        [696, 308, 992, 0, 114, 650, 878, 502, 844, 890, 1232, 514, 628, 822, 1164, 560, 1358],
        [582, 194, 878, 114, 0, 536, 764, 388, 730, 776, 1118, 400, 514, 708, 1050, 674, 1244],
        [274, 502, 502, 650, 536, 0, 228, 308, 194, 240, 582, 776, 662, 628, 514, 1050, 708],
        [502, 730, 274, 878, 764, 228, 0, 536, 194, 468, 354, 1004, 890, 856, 514, 1278, 480],
        [194, 354, 810, 502, 388, 308, 536, 0, 342, 388, 730, 468, 354, 320, 662, 742, 856],
        [308, 696, 468, 844, 730, 194, 194, 342, 0, 274, 388, 810, 696, 662, 320, 1084, 514],
        [194, 742, 742, 890, 776, 240, 468, 388, 274, 0, 342, 536, 422, 388, 274, 810, 468],
        [536, 1084, 400, 1232, 1118, 582, 354, 730, 388, 342, 0, 878, 764, 730, 388, 1152, 354],
        [502, 594, 1278, 514, 400, 776, 1004, 468, 810, 536, 878, 0, 114, 308, 650, 274, 844],
        [388, 480, 1164, 628, 514, 662, 890, 354, 696, 422, 764, 114, 0, 194, 536, 388, 730],
        [354, 674, 1130, 822, 708, 628, 856, 320, 662, 388, 730, 308, 194, 0, 342, 422, 536],
        [468, 1016, 788, 1164, 1050, 514, 514, 662, 320, 274, 388, 650, 536, 342, 0, 764, 194],
        [776, 868, 1552, 560, 674, 1050, 1278, 742, 1084, 810, 1152, 274, 388, 422, 764, 0, 798],
        [662, 1210, 754, 1358, 1244, 708, 480, 856, 514, 468, 354, 844, 730, 536, 194, 798, 0],
        # fmt: on
    ]
    data["num_vehicles"] = 4
    data["depot"] = 0
    return data


def print_solution(data, manager, routing, solution):
    """Prints solution on console."""
    print(f"Objective: {solution.ObjectiveValue()}")
    max_route_distance = 0
    for vehicle_id in range(data["num_vehicles"]):
        index = routing.Start(vehicle_id)
        plan_output = f"Route for vehicle {vehicle_id}:\n"
        route_distance = 0
        while not routing.IsEnd(index):
            plan_output += f" {manager.IndexToNode(index)} -> "
            previous_index = index
            index = solution.Value(routing.NextVar(index))
            route_distance += routing.GetArcCostForVehicle(
                previous_index, index, vehicle_id
            )
        plan_output += f"{manager.IndexToNode(index)}\n"
        plan_output += f"Distance of the route: {route_distance}m\n"
        print(plan_output)
        max_route_distance = max(route_distance, max_route_distance)
    print(f"Maximum of the route distances: {max_route_distance}m")


def main():
    """Entry point of the program."""
    # Instantiate the data problem.
    data = create_data_model()

    # Create the routing index manager.
    manager = pywrapcp.RoutingIndexManager(
        len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
    )

    # Create Routing Model.
    routing = pywrapcp.RoutingModel(manager)

    # Create and register a transit callback.
    def distance_callback(from_index, to_index):
        """Returns the distance between the two nodes."""
        # Convert from routing variable Index to distance matrix NodeIndex.
        from_node = manager.IndexToNode(from_index)
        to_node = manager.IndexToNode(to_index)
        return data["distance_matrix"][from_node][to_node]

    transit_callback_index = routing.RegisterTransitCallback(distance_callback)

    # Define cost of each arc.
    routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)

    # Add Distance constraint.
    dimension_name = "Distance"
    routing.AddDimension(
        transit_callback_index,
        0,  # no slack
        3000,  # vehicle maximum travel distance
        True,  # start cumul to zero
        dimension_name,
    )
    distance_dimension = routing.GetDimensionOrDie(dimension_name)
    distance_dimension.SetGlobalSpanCostCoefficient(100)

    # Setting first solution heuristic.
    search_parameters = pywrapcp.DefaultRoutingSearchParameters()
    search_parameters.first_solution_strategy = (
        routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
    )

    # Output log
    search_parameters.log_search = True

    # Solve the problem.
    solution = routing.SolveWithParameters(search_parameters)

    # Print solution on console.
    if solution:
        print_solution(data, manager, routing, solution)
    else:
        print("No solution found !")


if __name__ == "__main__":
    main()

The output of this code is as follows:

Read more »

Posted on Word count in article: 326 Reading time ≈ 1 mins.

UUID is usually used to generate unique identifiers, such as the ID field of the database, user account number, etc.

The following are some commonly used functions, for more information: https://docs.python.org/3/library/uuid.html.

uuid.uuid1(node=None, clock_seq=None)

Generate a UUID from a host ID, sequence number, and the current time. If node is not given, getnode() is used to obtain the hardware address. If clock_seq is given, it is used as the sequence number; otherwise a random 14-bit sequence number is chosen.

uuid.uuid3(namespace, name)

Read more »

Posted on Word count in article: 77 Reading time ≈ 1 mins.

Step 1: Find the hosts file from the following location: C:\windows\system32\drivers\etc, as shown in the figure below:

Step 2: Add records according to the format of "ip domain name", and the IP and domain name need to be separated by spaces, as shown below:

Note: You can open the hosts file as .txt file and modify it.

Read more »

Posted on Word count in article: 308 Reading time ≈ 1 mins.

The TSP problem usually requires finding a path with the minimum weight (or cost) that starts from the starting point, passes through all other nodes in sequence without repetition, and finally returns to the starting point

Parameter Description

Parameter Description
VV The collection of all nodes
nn Number of nodes
i,ji,j Node Number, i,j∈Vi,j \in V
cijc_{ij} The weight (or cost) of edge (i,j)(i,j)
xijx_{ij} 0-1 decision variable, where 1 means visiting edge (i, j) and 0 means not visiting edge (i, j)
Read more »

Posted on Word count in article: 563 Reading time ≈ 2 mins.

I have recently read some literature on truck scheduling in mining areas which is generally a combinatorial optimization problem. The following is a brief summary of a common scheduling model in the literature.

Parameter Description

Parameter Description Unit
ii Loading area number, i=1,⋯,mi=1,⋯,m —
jj Unloading area number, j=1,⋯,nj=1,⋯,n —
rr Truck number, r=1,⋯,Kr=1,⋯,K —
GG Total Target Mineral Production tt
TT Length of each work shift hh
KK Maximum number of trucks available —
CC Rated load capacity of each truck tt
tlt_l Average loading time of each truck hh
tut_u Average uninstall time of each truck hh
vfv_f Average speed of a fully loaded truck km/hkm/h
vev_e Average speed of an empty truck km/hkm/h
cfc_f The transportation cost per unit distance when the truck is fully loaded RMB/kmRMB/km
cec_e The transportation cost per unit distance when the truck is empty RMB/kmRMB/km
dijd_{ij} The shortest path distance from loading area ii to unloading area jj kmkm
fjf_j Requirements of unloading area jj tt
gig_i Total amount of minerals in loading area ii tt
hjh_j The maximum unloading amount of unloading area jj tt
BcB_c The maximum number of loading times at all loading points within one shift —
aia_i Mineral grade in loading area ii %
ee Desired mineral grade %
α\alpha Maximum allowed grade error %
xrijx_{rij} The number of full trips of truck rr from the loading area ii to the unloading area jj —
yrjiy_{rji} The number of empty trips of truck rr from the unloading area jj to the loading area ii —
Read more »

Posted on Edited on Word count in article: 1.1k Reading time ≈ 4 mins.

Deep Q-Network (DQN) is a deep reinforcement learning method, first proposed by Google DeepMind team in 2013 [Paper]. This algorithm introduces a neural network to replace the cumulative expected return storage form in the Q-learning algorithm, and can effectively solve problems with high-dimensional state spaces. The DeepMind team creatively combines convolutional neural networks in deep learning and Q-learning in reinforcement learning to train agents to learn how to control characters in Atari games to achieve good game performance.

Neural Network

The DQN algorithm takes the state of the agent as the input of the neural network, and then uses the neural network to calculate the Q values corresponding to all actions.

Online Network and Target Network

Read more »

Posted on Edited on Word count in article: 661 Reading time ≈ 2 mins.

This project is also part of my master's thesis, and it includes two aspects: global path planning of each robot and collaborative planning of multiple robots. My master's thesis (Written in Chinese) can be downloaded here.

Global Path Planning for Each Robot

Abstract:

To solve the routing problem in Mobile Robot Fulfillment System, firstly, a method based on traditional A* algorithm is proposed, and then a method based on improved A* algorithm considering task priority and utilization frequency of path nodes is further designed. Finally, a Markov decision process describing the problem is established, and a method based on Q-learning is proposed. Results of computational experiments show that these algorithms can quickly solve the problem. The methods based on the traditional A* algorithm and Q-learning can both obtain the shortest paths, and the method based on improved A* algorithm can effectively balance the traffic flow and significantly reduce the number of potential collisions.

Comparison between Traditional A* Algorithm and Improved A* Algorithm

Read more »
0%