Kruskal Algorithm for Finding the Minimum Spanning Tree
For obtaining the minimum spanning tree, the Prim algorithm has been introduced before, and here is another algorithm: Kruskal algorithm.
Kruskal Algorithm Steps
-
Step 1: Sorts all edges in the graph by weight from smallest to largest.
-
Step 2: Try adding edges to the tree from smallest to largest, and if the newly added edge forms a loop with other edges in the tree, discard the edge and continue trying the other edges.
-
Step 3: If edges are added to the tree, the minimum spanning tree is built, where is the number of vertices of the graph.
Note that in the process of adding edges to the tree, Disjoint Set Union (DSU) is used to determine if a loop is formed.
Example
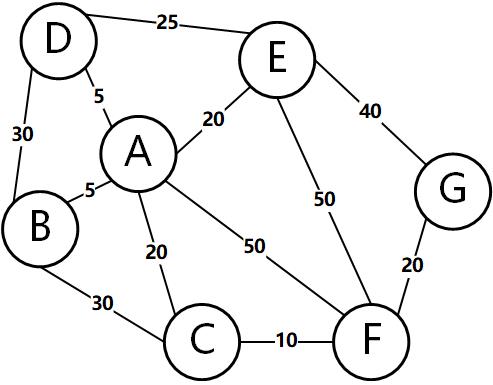
Take this undirected weighted graph above as an example to show the process of the Kruskal algorithm.
First, sort all edges in order of weight, from smallest to largest. Select the edge with the lowest weight which is here. If there are multiple edges with the lowest weight, select any one. As shown below:
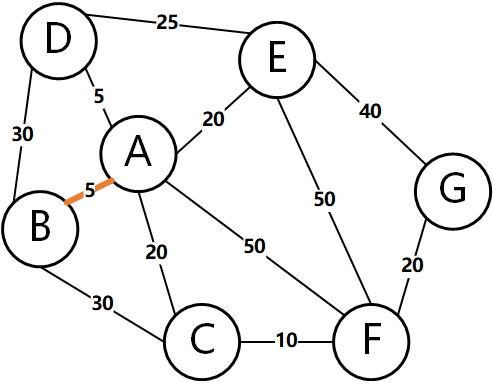
Then, select the edge with the lowest weight to add to the tree. As shown below:
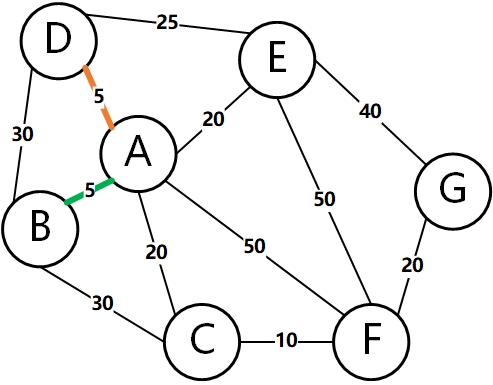
Then, select the edge with the lowest weight to add to the tree. As shown below:
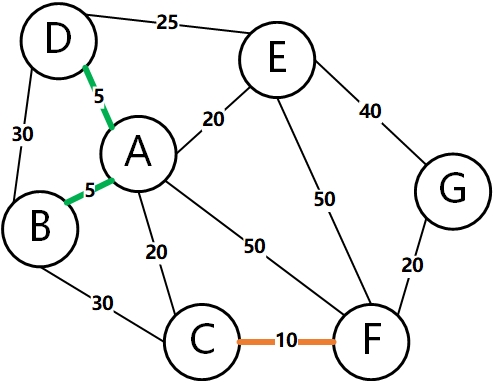
Then, select the edge with the lowest weight to add to the tree. As shown below:
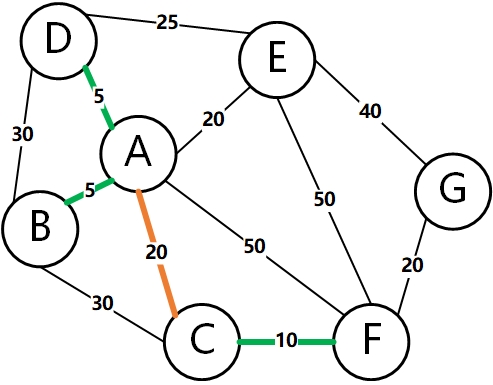
Then, select the edge with the lowest weight to add to the tree. As shown below:
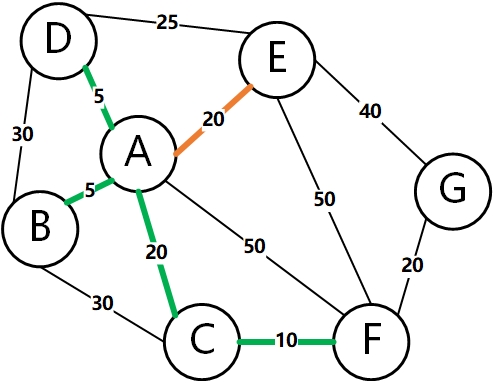
Then, select the edge with the lowest weight to add to the tree. The original graph had 7 vertices, and now there are 6 edges in the tree, so the minimum spanning tree is built. As shown below:
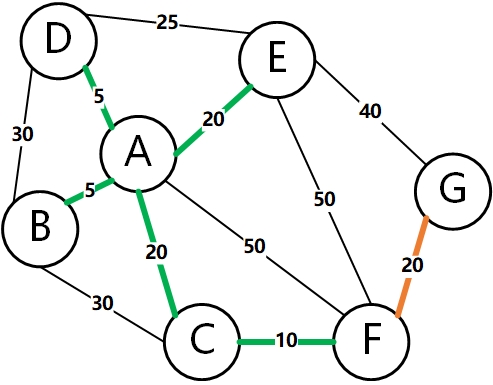
Finally, we can get the following minimum spanning tree:
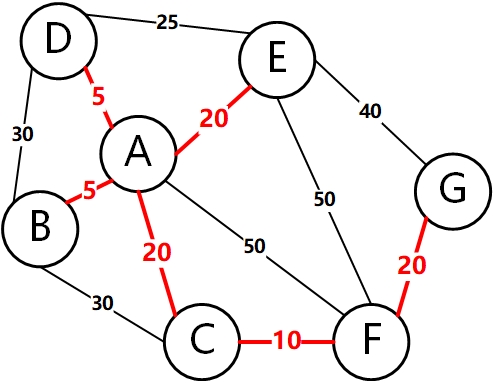
Code
The Kruskal algorithm is implemented using Python.
1 | import heapq |
The output is as follows:
1 | The edge with the lowest weight selected this time : A-B, weight: 5. Add it to the tree. |