Calculate the Angle Between Two Vectors in Python

Posted on Views: Word count in article: 309 Reading time ≈ 1 mins.

Formula

Given vectors AB⃗\vec{AB} and CD⃗\vec{CD}, A=(x1,y1)A=(x_1,y_1), B=(x2,y2)B=(x_2,y_2), C=(x3,y3)C=(x_3,y_3), D=(x4,y4)D=(x_4,y_4), then:

AB⃗=(x2−x1,y2−y1)CD⃗=(x4−x3,y4−y3)\vec{AB}=(x_2-x_1, y_2-y_1)\\ \vec{CD}=(x_4-x_3, y_4-y_3)

Let the angle between the vectors AB⃗\vec{AB} and CD⃗\vec{CD} be θ\theta:

cos(θ)=AB⃗⋅CD⃗∣∣AB⃗∣∣⋅∣∣CD⃗∣∣cos(\theta)=\frac{\vec{AB} \cdot \vec{CD}}{||\vec{AB}|| \cdot ||\vec{CD}||}

Code

The Python code for the formula is as follows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import math


class point():
    def __init__(self, id, x, y):
        self.id = id
        self.x = x
        self.y = y


# Start and end point of line 1
start_point_l1 = point("l1 start point", 2.4, 5.2)
end_point_l1 = point("l1 end point", 4.2, 3.1)

# Start and end point of line 2
start_point_l2 = point("l2 start point", 1.6, 3)
end_point_l2 = point("l2 end point", 6.2, 5.6)

delta_x = start_point_l1.x - end_point_l1.x
delta_y = start_point_l1.y - end_point_l1.y
delta_x_edge = start_point_l2.x - end_point_l2.x
delta_y_edge = start_point_l2.y - end_point_l2.y

cos_value = (delta_x * delta_x_edge + delta_y * delta_y_edge) \
            / (math.sqrt(delta_x * delta_x + delta_y * delta_y)
               * math.sqrt(delta_x_edge * delta_x_edge + delta_y_edge * delta_y_edge))

# The angle between two straight lines
currRoadAngle = math.degrees(math.acos(cos_value))
print("The angle between two straight lines: ", currRoadAngle)

Examples

1
The angle between two straight lines:  78.87459435824127
1
The angle between two straight lines:  42.91155696958662
1
The angle between two straight lines:  149.3002774491856
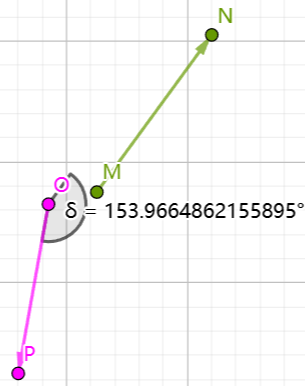
1
The angle between two straight lines:  153.9664862155895
1
The angle between two straight lines:  0.0
1
The angle between two straight lines:  90.0
1
The angle between two straight lines:  180.0